Mapping the Whole World in Hexes: Part I

The original Gamma World hex maps of North America were like magic in my brain. Here was something familiar, yet totally alien. You could throw anything together and call it a fantasy map, but if your campaign was based on real world places, the geography really meant something.

Now that I'm older, I've been wanting to re-do those maps with a little more accuracy, a little more (gasp!) realism. The problem with maps of big continent sized areas is that no matter how good they look, they are inherently wrong. The larger the area portrayed, the more distorted it has to be in order to be shown on a regular flat map. Consider this very familiar looking map:


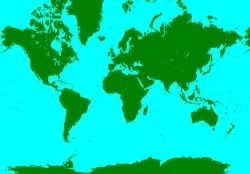
Greenland is really not that huge compared to the rest of North America, the areas in this projection are greatly exaggerated the further you get from the equator. If you took this map and just slapped a hex grid over it, it would be very, very wrong.

Now all maps are inherently wrong, but some much more than others. I'd like to have a map of the post-apocalyptic United States (and ultimately, the whole world) where at least the areas of the hexes in various locations are comparable to each other, if not exactly the same. Wouldn't you? So how do we go about doing it?

The Icosohedral World

First, we need a way to flatten the sphere of the world a bit so that we can get large flat areas for mapping. These areas can be unfolded and shown on a flat surface, and then folded up again to make an approximation of a spherical shape. We do this by turning the world into a big d20 (an icosohedron).

Each triangular face is flat, and a shape that can easily be broken up into smaller hexagons. The entire icosahedron can be unfolded into a pattern of connected triangles that looks like this:


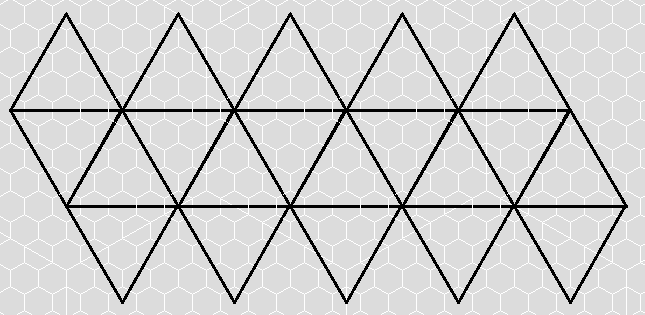
Our Triangular Face

The continental US fits reasonably well if we center one of the top triangular faces on the 96 degree West line of longitude. This makes the sides of the triangle the 132 degree and 60 degree longitudinal lines from left to right. The bottom of this triangle is the 30 degree North line of latitude. The US goes down further than 30 degrees, but that's fine for now. Since we aren't using all of the triangle above, we will also use only a part of the triangle below.

You can break up an equilateral triangle into a hex grid like so:


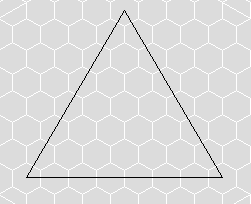
Notice that each line starting from the top has one more hex than the line previous and that there is the same number of hexes across the bottom as there is total rows of hexes. To find out how many hexes total there are on a triangle of X lines, the formula is (x * (x + 1)) / 2 or (x^2 + x) / 2. So for 1 line there is 1 hex, for two lines there are 3 hexes, for three lines there are 6 hexes, for 10 lines there are 55 hexes, etc.

A Sense of Scale

When finished, I want a map of the US broken up into 5 mile wide hexes (width from flat side to flat side). For a larger overview, however, I think I may use 50 mile wide hexes instead. To convert, 100 five mile hexes fit nicely into a single 50 mile hex like this:


But just exactly how big is the triangular face we will be using for our map? How many hexes is it across the bottom at the 30 degree North line, how many hexes across is the top of our map at the 50 degree North line, and how many total hexes are there?There's a couple of ways to figure this out, but one way in particular is the one I'm going to use.

...and that is where we will have to stop until next time. Stay tuned!